Babys N-gram

Matt Allen

2024-05-21

Introduction

• Focus of this talk is on N-gram Models

• N-gram models were used as a benchmark that the Neural Probabilistic Language Model aimed to surpass

• Future talk on Neural Network based Language Models NPLM or Transformer

This talk is on N-Gram models. They are perhaps the first language model going all the way back to Markov in 1913, and continued to be developed into the 2000’s when Neural Network based language modeling came into vogue.

N-Grams models are worth studying to develop intuition on how autoregressive language models work and what problems Neural Networks solve.

Future talk on NN based Language Models, but to start we will look at an early language model called N-gram.

Example code and data from Presentation

Baby’s N-Gram Model Presentation to Deep Learners Paper Reading Group 5/18/2024

Purpose

• Understand paper by implementing models from it

• Learn Language Modeling concepts like Training and Test Sets, Tokenization, Sampling and Model Evaluation

The best way for me to understand models in AI papers is to implement them. We will implement four variations of the N-Gram model. Along the way, we will use language modeling concepts like training and test sets, tokenization, model sampling and model evaluation.

Language Model Definition

• A Model that assigns probabilities to upcoming words or sequences of words.
  • Can also assign probabilities to sentences
  • Next word (token) guesser

Depending on who you talk to, either next word guesser or the thing that will end civilization as we know it.

Language Model Applications

• Autocomplete on phone keyboard
• Writing assitant to help choose better sentences
• GPT Large Language Model (LLM) at the core of Chat GPT
• Augmentative and Alternative Communication (AAC) Systems
• Translators

Chat GPT is composed of several models, but at the heart of it is GPT (generative pre-trained transformer), which is a next word guesser. We will be building a comparatively simple next word guesser.

AAC Systems give voice to those who cannot speak or sign. Predict next word with eye movements.

N-Gram

• Defn 1: Sequence of N words
  • 2-Gram is called a Bigram
  • 3-Gram is called a Trigram
• Example:
  • My puppy
  • My puppy is

N-Gram

• Defn 2: Probabilistic Model that estimates probability of a word given N-1 previous words
  • Bigram Model uses 1 word (token) to predict the next word
  • Trigram Model uses 2 words (tokens) to predict the next word

Probability Crash Course

• Probability is a number between 0 and 1 inclusive
  • 0 means no chance and 1 means absolute certainty

Probability Crash Course

• Probability distribution is a function that takes an event as input and outputs a probability
  • Example Fair Coin Flip \[\mathrm P( X = Heads ) = 0.5 \]
  • Sum of all probabilities of the mutually exclusive events of the probability distribution sum to 1 \[\mathrm P( X = Heads ) + P( X = Tails ) = 1 \]

Probability Crash Course

• Conditional Probability Distribution is a probability distribution notated as \[\mathrm P( Y = y | X = x ) \]
  • Read as probability of Y given X
  • Now that X has happened what is the probability of Y

N-Gram Model Training

Bigram Example

\[\mathrm P( dog | the ) = \dfrac{C(the\;dog)}{C(the)} \]

Trigram Example

\[\mathrm P( dog | the\;small ) = \dfrac{C(the\;small\;dog)}{C(the\;small)}\]

This slide has example conditional probability distributions relevant to N-Grams.

To compute the Bigram Probability, we simply count all occurrences of “the” in a training corpus and “the small”, then divide them.

Corpus: A collection of written text. This could be Shakespeare, Wall Street Journal or a list of Baby Names.

Markov Assumption

• Markov models are the class of probabilistic models that assume we can predict the probability of some future unit without looking too far into the past. ¹

The last few words are enough to predict the next word.

Speech and Language Processing. Daniel Jurafsky & James H. Martin. Copyright © 2023. All rights reserved. Draft of February 3, 2024.

1. Chapter 3

Markov Assumption

\[\mathrm P(w_{n}|w_{1:n-1}) \approx \mathrm P(w_{n}|w_{n-N+1:n-1})\]

This is the Markov Assumption expressed formally.

You can see having an extra word of context in the Trigram example can really narrow down the possibilities.

Bigram Example: N = 2, n = 6

\[\mathrm P( stairs | a\;schnauzer\;walks\;up\;the ) \approx \mathrm P( stairs | the ) \]

Trigram Example: N = 3, n = 6

\[\mathrm P( stairs | a\;schnauzer\;walks\;up\;the ) \approx \mathrm P( stairs | up\;the ) \]

The N-Gram intuition is that instead of viewing entire sequence of words that led up to a word, we can approximate probability with the last few words. The last few are the most important.

You can see in this case having an extra word (more context) can really help. A lot of words could follow “the”, but “up the” narrows it down quite a bit.

Application: Baby Name Generator

• Build Generative Bigram and Trigram Models that make new First names

• Data Source: Social Security Administration Baby Names

  • Downloaded Zip file that contains file for every year from 1880 to 2022

To build a name generator, use names for your dataset! Models trained on Shakespeare will generate Shakespeare like text or WSJ will produce WSJ text.

We use baby names from Social Security Administration to Generate Names.

Data

• Each file represents a year and each row has format:

  • Name,Gender,Registrations
  • Stephanie,F,22775

• Wrote Code to read in all the files and write out unique names in lowercase to file like

  • stephanie

Open GitHub and show all the data files.

View the Data

total number of names: 102449

random sample of 5 names:  ['padraic', 'juleanna', 'amyrion', 'xaylen', 'latash']


min length word: 2

max length word: 15

View the Data

shortest_names: ['ii', 'ja', 'vi', 'od', 'kd', 'ax', 'jd', 'jp', 'st', 'sa', 'rc', 'jt', 'xi', 'ju', 'zy', 'mi', 'kj', 'cj', 'ho', 'se', 'io', 'ge', 'eh', 'jw', 'un', 'kc', 'no', 'an', 'mr', 'va', 'oz', 'du', 'ji', 'ah', 'tr', 'mc', 'si', 'zi', 'ld', 'go', 'pj', 'la', 'qi', 'jm', 'or', 'bj', 'sy', 'lu', 'ao', 'zo', 'su', 'ed', 'xu', 'za', 'ra', 'bb', 'na', 'ry', 'ki', 'pa', 'gy', 'md', 'vu', 'fu', 'ti', 'lj', 'jo', 'ad', 'ej', 'di', 'jl', 'my', 'ku', 'mu', 'lc', 'vy', 'te', 'ar', 'aj', 'ze', 'rb', 'ly', 'jc', 'el', 'so', 'ya', 'ma', 'gi', 'ia', 'yu', 'po', 'li', 'ac', 'lb', 'sj', 'tu', 'ke', 'fe', 'ro', 'kt', 'dj', 'al', 'eb', 'wa', 'mj', 'ab', 'oh', 'rj', 'tc', 'je', 'hy', 'lg', 'yi', 'om', 'yy', 'oc', 'ty', 'me', 'ko', 'av', 'ny', 'ng', 'yo', 'ai', 'jb', 'ka', 'jj', 'ru', 'ea', 'ni', 'ky', 'da', 'rd', 'de', 'le', 'bo', 'do', 'ta', 'rl', 'jr', 'ye', 'in', 'mo', 'ok', 'wc', 'hu', 'wm', 'ha', 'bg', 'ba', 'be', 'lo', 'cy', 'tj', 'en']

View the Data

longest_names: ['laurenelizabeth', 'ryanchristopher', 'christianjoseph', 'sophiaelizabeth', 'mariadelosangel', 'michaelchristop', 'ashleyelizabeth', 'johnchristopher', 'muhammadibrahim', 'jordanalexander', 'joshuaalexander', 'christophermich', 'christopherpaul', 'christianmichae', 'christianalexan', 'jonathanmichael', 'christiandaniel', 'davidchristophe', 'gabrielalexande', 'christopherdavi', 'mariadelrosario', 'christopherjose', 'christopherjohn', 'jordanchristoph', 'markchristopher', 'seanchristopher', 'christopheranth', 'kevinchristophe', 'christopherjame', 'jaydenalexander', 'christiananthon', 'christopherryan', 'muhammadmustafa', 'franciscojavier', 'hannahelizabeth', 'christianjoshua', 'matthewalexande']

Tokenizer

• Tokenizers change text to numbers for computers
  • Break text in a corpus up into words or word parts to create a vocabulary

Corpus: A collection of written text. This could be Shakespeare, Wall Street Journal or a list of Baby Names.

Tokenizer

• We will use a simple tokenizer with vocabulary size 27:
  • 26 lowercase letters and “.” to denote beginning and ending of words
  • Create two mappings:
    • Encode for computers: Text to Integers
    • Decode for humans: Integers to Text

Tokenizer

tokens: ['.', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']

stoi: {'.': 0, 'a': 1, 'b': 2, 'c': 3, 'd': 4, 'e': 5, 'f': 6, 'g': 7, 'h': 8, 'i': 9, 'j': 10, 'k': 11, 'l': 12, 'm': 13, 'n': 14, 'o': 15, 'p': 16, 'q': 17, 'r': 18, 's': 19, 't': 20, 'u': 21, 'v': 22, 'w': 23, 'x': 24, 'y': 25, 'z': 26}

itos: {0: '.', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}

Data Split

• Motivation: Want model to do well on unseen data otherwise could simply memorize

• Procedure: Shuffle data randomly split 80% Training, 10% Dev/Validation, 10% Test

Data Split

• Purpose:
  • Training Set Used to Train the model
  • Development / Validation Set Used to Tune Hyperparameters and as a Practice Test Set
  • Test Set Used as Final judge to be used once or sparingly
    • Every time use test set at risk of fitting to it

Using test set more than once risks fitting to it. You may for example see a bad result then go back and tweak the model to make the test set performance better, but you want performance on unseen data.

Data Split

Xtr shape: torch.Size([616858, 1]) Ytr shape:  torch.Size([616858])

Xdev shape: torch.Size([77121, 1]) Ydev shape:  torch.Size([77121])

Xte shape: torch.Size([77050, 1]) Yte shape:  torch.Size([77050])

Transformed data: 4 Gram Example

matt
input ---> output
... ---> m
..m ---> a
.ma ---> t
mat ---> t
att ---> .
kathy
input ---> output
... ---> k
..k ---> a
.ka ---> t
kat ---> h
ath ---> y
thy ---> .

Transformed data: 4 Gram Example

(tensor([[ 0,  0,  0],
        [ 0,  0, 13],
        [ 0, 13,  1],
        [13,  1, 20],
        [ 1, 20, 20],
        [ 0,  0,  0],
        [ 0,  0, 11],
        [ 0, 11,  1],
        [11,  1, 20],
        [ 1, 20,  8],
        [20,  8, 25]]), tensor([13,  1, 20, 20,  0, 11,  1, 20,  8, 25,  0]))

Transformed data: Trigram Example

matt
input ---> output
.. ---> m
.m ---> a
ma ---> t
at ---> t
tt ---> .
kathy
input ---> output
.. ---> k
.k ---> a
ka ---> t
at ---> h
th ---> y
hy ---> .

Transformed data: Trigram Example

(tensor([[ 0,  0],
        [ 0, 13],
        [13,  1],
        [ 1, 20],
        [20, 20],
        [ 0,  0],
        [ 0, 11],
        [11,  1],
        [ 1, 20],
        [20,  8],
        [ 8, 25]]), tensor([13,  1, 20, 20,  0, 11,  1, 20,  8, 25,  0]))

Transformed data: Bigram Example

matt
input ---> output
. ---> m
m ---> a
a ---> t
t ---> t
t ---> .
kathy
input ---> output
. ---> k
k ---> a
a ---> t
t ---> h
h ---> y
y ---> .

Transformed data: Bigram Example

(tensor([[ 0],
        [13],
        [ 1],
        [20],
        [20],
        [ 0],
        [11],
        [ 1],
        [20],
        [ 8],
        [25]]), tensor([13,  1, 20, 20,  0, 11,  1, 20,  8, 25,  0]))

Build the Bigram Model

• Maximum Likelihood Estimation (MLE)
  • Get counts of all two letter combinations from corpus and normalize to be between 0 and 1

Get MLE estimate for the parameters by getting counts from a corpus and normalizing the counts to be between 0 and 1.

This is called Maximum Likelihood Estimation.

Example Bigram Training (MLE)

\[\mathrm P( m | . ) = \dfrac{C(.m)}{C(.)} \] \[\mathrm P( a | m ) = \dfrac{C(ma)}{C(m)} \] \[\mathrm P( t | a ) = \dfrac{C(at)}{C(a)} \] \[\mathrm P( t | t ) = \dfrac{C(tt)}{C(t)} \]

Write out Counts Equation. Provide example bigram. Show table on next slide. Emphasize that training set was used. C is for Count. The sum of each row in the table is for example C(.). Each cell is C(.m) for example

Count of denominator is unigram. It is the same thing as the letter combined with every other character.

Each row will be a conditional probability distribution. It is conditioned on the left most character.

Every cell in a row is a disjoint event. ma is a different event than me. Think of these letter combinations as the disjoint event in heads and tails, but now instead of 2 possibilities there are 27.

Normalize all values in row by sum of row so that row sums to 1. This makes each row a probability distribution conditioned on the left most character.

These 27 conditional probability distributions are what we will use to generate next characters to build up new names.

For example, suppose the model has generated the sequence “matt”.

Imagine that every row in this matrix of counts is normalized by the sum of the row. We can also look at the plots on GitHub to see what the actual distributions look like.

Trace through “matt” example.

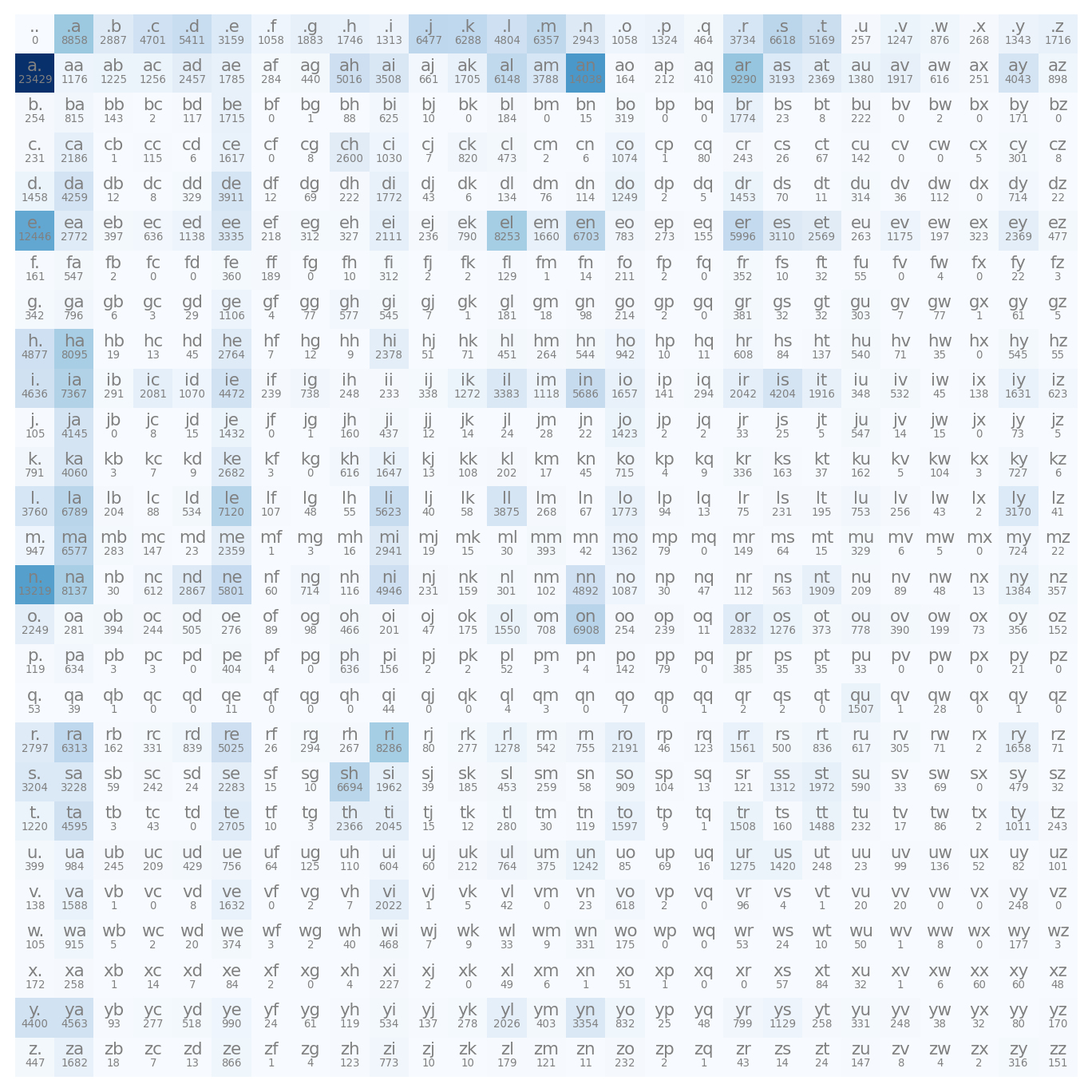
Build the Bigram Model

• Notice some letter combinations are 0 in training set
• Possible that the letter combination occurs in the Test set
  • Will assign 0 probability if occurs in the test set
• Want all combinations to have some probability

Methods to Fix 0s by Smoothing or Discounting

• Add-one (Laplace) Smoothing
• Add-k Smoothing
• Backoff and Interpolation

Consequence of all Methods

• Moves probability distribution from more probable to the least probable.
• Example Add-one (Laplace) Smoothing: \[\dfrac{C(kg) + 1}{C(k) + 27} \]
• Use Add-one smoothing for now

Note that because these are probability distributions everything always has to sum to 1, so if we add something to one place we need to take it away from another.

Evaluating performance: Extrinsic Evaluation

• Evaluate Model within an end to end application like translation app
• Example: Expert rates English to French Translations
  • High quality but expensive

Best way to see how the model performs is to evaluate it within an application

Name generator informal Extrinsic evaluation (baseline)

• Let’s generate names where every character has equal probability

hbohpcfjzvvwrumsecaoredkgxejuyjpvtuggorcfape.
hxxvonrlozjg.
qsqyhbaxdmgottggxberspdqxgyjkkgnqjfimzz.
zlfmxezajcul.
ztitsggjrzjbykeprbbywxkyozuxhyebyptnjfvbakoqouizlwmpourdiobwwpctuabi.
.
deuyterurdref.
.
wturxgpqflwnxmuhkzarpjhhybdnyjmrtwapxbksnozrpnzcifezpkqumqorvuiyuhokyvebtiolsqbagskfachlaocmipeyyzkaepdyvqquvjgnxudgzqpnlyroznlgsodjhtjchjcjzghkgkodjbyvgawjmadt.
twdpdbfemevpomboztiefyyljlizeqdgzavgckyjdmiejucumxgbecdim.

Builds names by drawing samples from multinomial distribution (multiple discrete events). 27 possible next characters to choose from.

Think of a multinomial distribution as the coin flipping example except now instead of 2 possibilities there are 27.

In this case of all next characters equally likely, every character has a 1/27 chance of being chose. 27 is the size of our vocabulary.

The multinomial distributions are created from the conditional distributions we created earlier.

The output looks either too long or too short and looks gibberish.

Name generator informal Extrinsic evaluation

• Let’s generate names where next character probability has been estimated by data

shoh.
ca.
kiverumye.
a.
ridigele.
ynn.
angelycamae.
han.
tar.
o.

The length of the names looks right. The words look like names. Some may actually be names in the training set.

Intrinsic Evaluation

• Evaluate quality of the model independent of application by calculating a metric
• Examples: Perplexity or Average Negative Log Likelihood (Cross Entropy)
  • Low Perplexity and Cross Entropy guarantees a model is confident not accurate
  • Often correlates with model’s real world performance (extrinsic evaluation)

We don’t have to go in depth with these metrics. Just know that for both Cross Entropy and Perplexity, lower is better.

perplexity = (base used in cross entropy like 2 or e)^(NLL)

Evaluating performance: Intrinsic Evaluation

• Use Average Negative Log Likelihood (Cross Entropy)
• Compute using Dev or Test Set of Words (Unseen Data)

Cross Entropy Metric Lower is Better

• Bigram Next Character Equal Probability

training set loss
average negative log likelihood loss=3.2761025428771973
perplexity=26.472396348577874

dev set loss
average negative log likelihood loss=3.2966854572296143
perplexity=27.02292168727854

• Bigram Next Character Maximum Likelihood Estimation

training set loss
average negative log likelihood loss=2.4615585803985596
perplexity=11.723068653709893

dev set loss
average negative log likelihood loss=2.46355938911438
perplexity=11.746547752408356

Application: Add-one Bigram perplexity of matthew misspellings

• Misspelled letters near the correct letter on the keyboard

matthew
average negative log likelihood loss=2.8680849075317383
perplexity=17.60327400106397

mqtthew
average negative log likelihood loss=4.442142486572266
perplexity=84.95676555609052

mztthew
average negative log likelihood loss=3.786203384399414
perplexity=44.088694295287944

mztthww
average negative log likelihood loss=4.33640193939209
perplexity=76.43203689713529

matyhew
average negative log likelihood loss=3.3009164333343506
perplexity=27.137497235501396

Trigram Model

• Let’s see if Trigram Model does better

Build the Trigram Dataset

shanquell
input ---> output
.. ---> s
.s ---> h
sh ---> a
ha ---> n
an ---> q
nq ---> u
qu ---> e
ue ---> l
el ---> l
ll ---> .
latyra
input ---> output
.. ---> l
.l ---> a
la ---> t
at ---> y
ty ---> r
yr ---> a
ra ---> .

Do Maximum Likelihood Estimation

• Get counts of all three letter combinations
• We will now have a cube of probabilities
• Conditional distribution for every 2 letter combination

torch.Size([27, 27, 27])

Generate Names from Trigram Model

shonta.
javi.
rumie.
amice.
gilberia.
aughtri.
ane.
huavon.
loyce.
conya.

Cross Entropy Metric Lower is Better

• Add-one Trigram

training set loss
average negative log likelihood loss=2.1367483139038086
perplexity=8.471845011300763

dev set loss
average negative log likelihood loss=2.147836685180664
perplexity=8.566306719579961

Application: Add-one Trigram perplexity of matthew misspellings

• Misspelled letters near the correct letter on the keyboard

matthew
average negative log likelihood loss=2.562378406524658
perplexity=12.966620564651786

mqtthew
average negative log likelihood loss=3.8060429096221924
perplexity=44.972127528840815

mztthew
average negative log likelihood loss=3.982038736343384
perplexity=53.62625264611053

mztthww
average negative log likelihood loss=4.8572163581848145
perplexity=128.66554436216273

matyhew
average negative log likelihood loss=2.7988085746765137
perplexity=16.42506586940549

Add-k smoothing estimation

• Let’s see if tuning the amount we add to every cell improves performance

• First Trigram model used Add-one (Laplace) Smoothing

• Search for k that has the lowest loss on the Dev Set

Add-k smoothing estimation

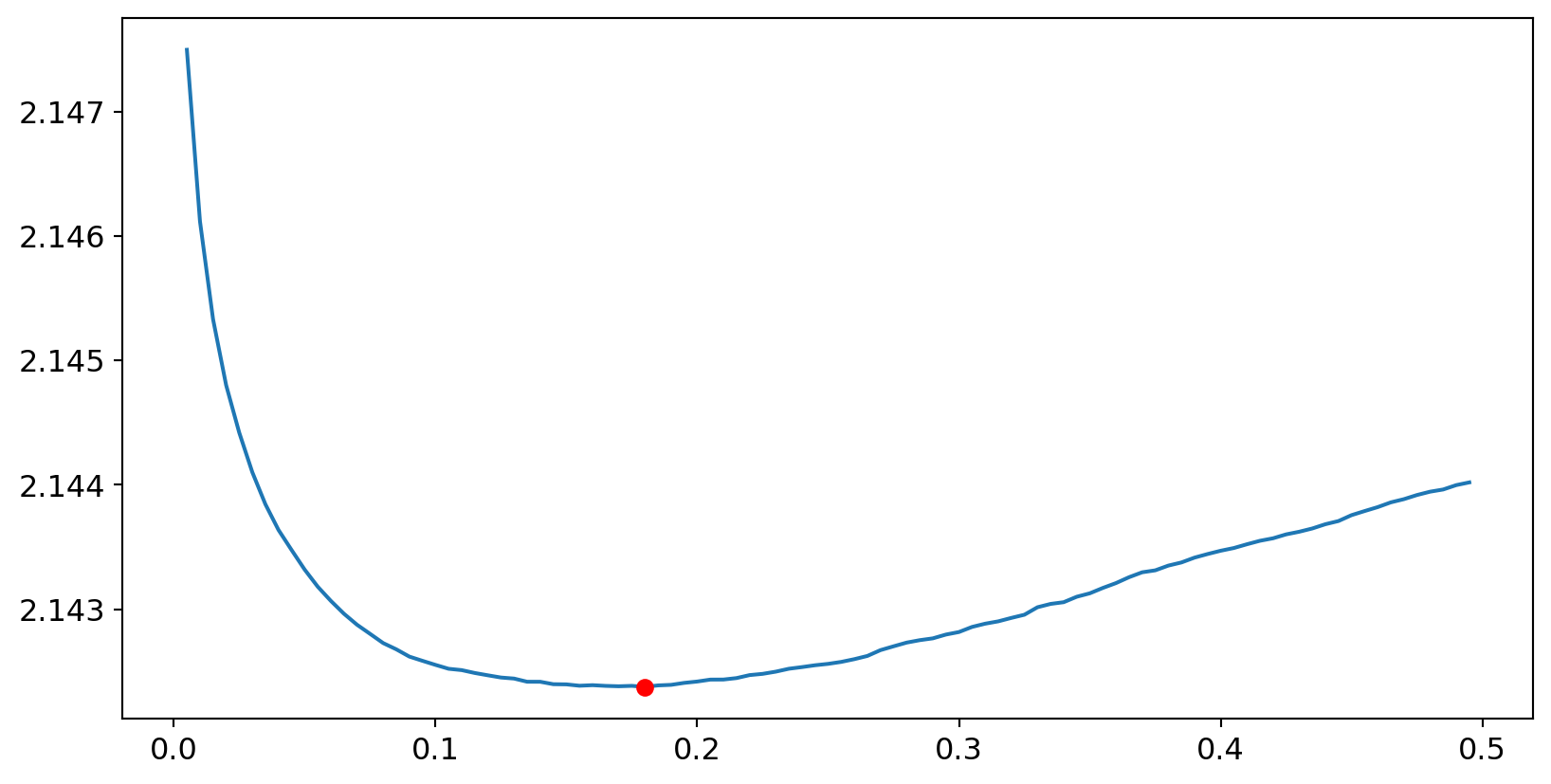
Add-k smoothing estimation

k with the lowest loss is 0.18

Model Generation for Add-k Smoothing

shonta.
javi.
rumie.
amice.
gilberia.
aughtri.
ane.
huavon.
loyce.
conya.

The name generation looks the same as the Add-1 trigram generation. The name generation is a random process, but you can set a seed to make it deterministic.

It is good to let it be random, so that you can get a feel for what the model outputs, but set a seed when you want results to be reproducible.

Does Add-k trigram model improve the loss?

• Dev Set Loss is a little lower compared to Add-one Trigram

training set loss on Add-k trigram
average negative log likelihood loss=2.127807855606079
perplexity=8.396440412376544

dev set loss on Add-k trigram
average negative log likelihood loss=2.1423745155334473
perplexity=8.519643655829894

dev set loss on Add-one trigram
average negative log likelihood loss=2.147836685180664

Application: Add-k Trigram perplexity of matthew misspellings

• Misspelled letters near the correct letter on the keyboard

matthew
average negative log likelihood loss=2.551401376724243
perplexity=12.825063941343927

mqtthew
average negative log likelihood loss=4.040593147277832
perplexity=56.86005919441688

mztthew
average negative log likelihood loss=4.539309978485107
perplexity=93.62617375100058

mztthww
average negative log likelihood loss=5.733122825622559
perplexity=308.9325059283187

matyhew
average negative log likelihood loss=2.7741856575012207
perplexity=16.025571376665223

Do Final evaluation on the test set

• Let’s choose the Trigram with Add-k Smoothing to be the final model

  • It has the lowest Dev Set Loss
  • Does better on misspellings task

• We’ve held out our Test Set until now

• Calculate loss to be reported for our chosen model on the Test Set

test set loss
average negative log likelihood loss=2.1444311141967773
perplexity=8.537183173276498

Drawbacks to N-gram Model

• Number of parameters grows exponentially with context
  • \[Bigram: 27^2, Trigram: 27^3, ..., N-gram: 27^N\]

Drawbacks to N-gram Model

• Does not take into account similarity between words
  • Having seen “The cat is walking in the bedroom” in the training corpus should generalize to make “A dog was running in a room” almost as likely.
  • “dog” and “cat”, “the” and “a”, “room” and “bedroom” have similar semantic and grammatical roles ¹
  • N-gram has no mechanism to generalize

Quoted from:

1. Neural Probabilistic Language Model

Neural Network Language Models Solve these issues and more

• Neural Probabilistic Language Model added ability to handle larger contexts and to generalize through embeddings

• Attention Layers described in Attention Is All You Need added ability to model relationships between words within the context

Describe embeddings. Space of words that through learning similar words move closer together in space.

Example sentences for attention from Attention in transformers, visually explained | Chapter 6, Deep Learning

American shrew mole

One mole of carbon dioxide

Take a biopsy of the mole

Attention in transformers, visually explained | Chapter 6, Deep Learning

Conclusion

• Defined Language Models

• Implemented a Bigram and Trigram Model

• Created Training and Test sets

• Evaluated Models Extrinsically and Instrinsically

• Implemented two Smoothing Techniques

Further Learning

• Neural Networks Zero to Hero

• Speech and Language Processing

• Practical Deep Learning for Coders